2023-03-13
Bra medelvärden, i genomsnitt?

Vi hanterar alla genomsnitt varje dag utan att ens tänka på det: har det varit kallt idag, har det varit blåsigt? Vi bildar intuitivt den totala upplevda medeltemperaturen eller vindhastigheten för att svara ja eller nej på dessa frågor.
Om det behövs kan vi också beräkna ett mer exakt genomsnitt: anteckna temperaturen som visas på en termometer, låt oss säga varje timme, addera värdena och dela med antalet timmar som du lyckades hålla dig vaken för att anteckna. Det lär vi oss alla i skolan, och vi kanske till och med har lärt oss att det kallas "aritmetiskt medelvärde".
Där det kan gå fel
Så vad är problemet när det gäller luftkvalitet och meteorologi? Låt oss titta på medelvärdet av en vindriktning, och låt oss säga att vi har noterat den en gång i timmen under de senaste 24 timmarna. Vad är det dagliga genomsnittet? Om man inte stannar upp och tänker efter så adderar du kanske bara de 24 riktningarna och delar med 24. Det kan ge rätt värde, men det kan också bli väldigt fel.
Säg att vinden var mellan nord och nordost halva dagen (0 till 45 grader i förhållande till sitt ursprung) och mellan nord och nordväst den andra halvan (315-360 grader). Den genomsnittliga riktningen är intuitivt något nära norr, men om man bara bildar det aritmetiska medelvärdet får man något nära 180 grader vilket tyder på sydliga vindar.
Det är uppenbart att vi inte kan beräkna en genomsnittlig vindriktning som ett aritmetiskt medelvärde och anledningen är att riktningsavläsningen 359,9 följs direkt av 0,0. Vi måste i stället förlita oss på vektoriserad medelvärdesbildning.
Vektoriserad medelvärdesbildning
En vektor är en pil, för att uttrycka det enkelt. Den har en längd och en riktning, och dessa två egenskaper kan inte skiljas åt eftersom man då förlorar delar av informationen om pilen. "Vind" är också en vektor där längden är vindhastigheten och orienteringen är vindriktningen. I själva verket är det en tredimensionell vektor eftersom det vanligtvis finns både horisontella och vertikala vindkomponenter, men låt oss bortse från det för tillfället och bara tänka på det i två dimensioner, som ovanpå en karta. De två siffrorna (hastighet och riktning) måste hållas samman för att ge en fullständig bild.
För att beräkna den genomsnittliga vindriktningen måste man lägga ihop de enskilda "vindpilarna" och se vart den resulterande pilen pekar. Matematiskt gör man det genom att införa ett koordinatsystem där till exempel x-axeln är den öst-västliga riktningen och y-axeln är den syd-nordliga riktningen.
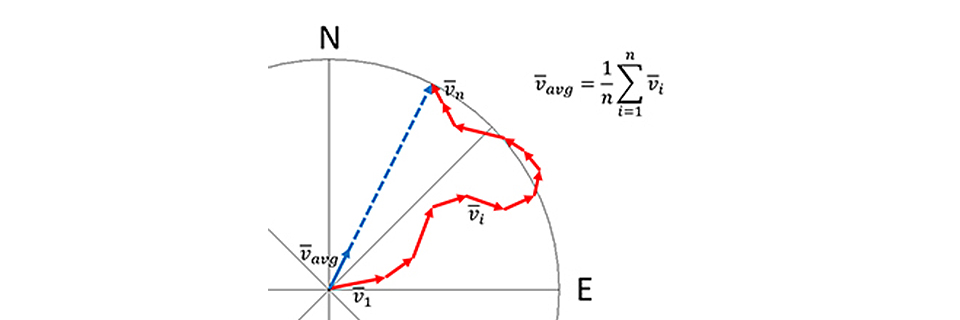
Beräkna nu det aritmetiska medelvärdet av projektionen av de enskilda vindpilarna på x- respektive y-axeln. Den genomsnittliga vindriktningen är sedan arcus-tangenten av kvoten av resulterande y-axel- och x-axelkomponenterna. Man måste hantera fallet där x-axelns komponent närmar sig noll (vänd på kvoten) och ta hand om vissa frågor om vinkelförskjutning och riktning, men det är enkel addition och subtraktion.
De viktade resultaten
Vad vi får med denna vektorbaserade beräkning är den "vindhastighetsviktade genomsnittliga vindriktningen". Samtidigt ger Pythagoras sats oss enkelt också den "vindriktningsvägda medelvindhastigheten". Det här är vad du bör titta på om du vill se hur luftvolymen har rört sig från början till slut av medelvärdestiden, och det är ofta det som är relevant för att studera hur luftföroreningar rör sig från sina källor.
Praktisk användning, genvägar
Programvara för studier av tidsserier av luftkvalitetsdata inklusive vinddata bör ha en inställning som möjliggör vektoriserad medelvärdesbildning för åtminstone vindriktningen (enhetsvektor) och helst för paret vindhastighet och vindriktning (sann vektoriserad medelvärdesbildning).
Om vi bara har de ursprungliga riktningsuppgifterna utan några hastighetsuppgifter kan vi ändå beräkna en vektormedelvärdesriktning. Det görs med en vektor med enhetslängd (längd 1), vilket innebär att vi antar att vindhastigheten förblir densamma under medelvärdestiden. Det ger inte exakt samma riktningsmedelvärde som det vindhastighetsviktade medelvärdet, men det kan vara tillräckligt bra, åtminstone för kortare medelvärdesperioder. Ett aritmetiskt medelvärde av vindriktningsdata är dock bara felaktig datahantering.
Hur man upptäcker felaktig medelvärdesberäkning
Felaktig medelvärdesbildning kan ibland avslöjas genom att man tittar på frekvensfördelningen av rapporterade medelvindriktningar under en längre tid. Om det finns märkligt få observationer i ett tillräckligt smalt nordligt segment jämfört med angränsande segment medan sydliga riktningar verkar överrepresenterade så bör man ta en närmare titt på matematiken. Det kan naturligtvis finnas naturliga förklaringar men det skadar inte att dubbelkolla om "vektorflaggan" verkligen var aktiverad när medelvärdena bildades.
Vindhastighetsdata kan också beräknas som ett vanligt aritmetiskt medelvärde. Detta ger den upplevda vindhastigheten, utan hänsyn till eventuella förändringar i vindriktningen. Skillnaden jämfört med den vektormedelvärdesberäknade hastigheten kan vara stor. I ett extremt (men orealistiskt) fall med östlig storm under halva medelvärdestiden och västlig storm under andra halvan, är den vektormedelvärdesberäknade hastigheten noll, men vi har säkert känt av det aritmetiska medelvärdet - det har blåst!
