2021-03-16

Inuti gasanalysatorn - interferometern

Flera av OPSIS gasanalysatortyper använder DOAS-tekniken för att fastställa koncentrationen av gaser. För att göra detta behöver vi tillgång till absorptionsspektra i olika våglängdsområden. Ett ganska okomplicerat sätt att registrera spektra är att använda en spektrometer.

Spektrometern är dock i allmänhet bäst i ultravioletta (UV) och synliga våglängdsområden. Den kan också användas i det infraröda (IR) våglängdsområdet, men det är svårt att få den spektrala upplösning som krävs för detektering av riktigt låga gaskoncentrationer. Ibland behövs det inte och då erbjuder OPSIS spektrometerbaserade analysatorer som arbetar i IR-området. I andra fall är det inte tillräckligt. Lyckligtvis finns det en lösning - interferometern.

Det är här som det blir lite knepigt. Det är ganska lätt att förstå vad ett "spektrum" är. Vi har alla sett en regnbåge, och det är ett exempel på ett spektrum. Att fundera över ett spektrum i andra än synliga våglängder eller "upplösningen" av ett spektrum är också ganska enkelt. Allt bygger på att vi uppfattar ljus som elektromagnetiska vågor, med olika våglängder för olika färger i spektrumet.

Våglängd vs. frekvens

Det finns dock olika sätt att beskriva och mäta ljus. Ett sätt är att betrakta ljus som partiklar, s.k. fotoner. Ett annat sätt är att hålla fast vid den våglängdsbaserade beskrivningen, men i stället titta på "våglängdernas invers". Det låter kanske konstigt, men vi känner alla igen tillvägagångssättet från en annan typ av elektromagnetiska vågor: radiosignaler. Till exempel pratar vi ofta om frekvensen ("f") för radiostationer som är inställda på en FM-radio, vanligtvis runt 100 MHz. Men vi kan lika gärna tala om våglängden ("L") för radiosändningen. Vi kan till och med se våglängden på en gammaldags radiomottagare: antennen är ofta strax under en meter lång. Det är en antennkonstruktion som kallas "kvartsvågsantenn". Våglängden är alltså fyra gånger så lång som antennen, cirka 3 meter. Samma radiosändning kan alltså beskrivas antingen som "100 MHz" eller som "3 m". Kopplingen mellan f och L är den fasta ljushastigheten ("c", 300 000 km/s): f = c / L.

På samma sätt fungerar det med elektromagnetiska vågor i det optiska området. Det vi beskriver som en våglängd i t.ex. IR-området (ofta angivet i mikrometer) kan lika gärna beskrivas som en frekvens. Det ger en mycket hög frekvens, i terahertz (THz)-området eller högre, men det är en frekvens. För att göra siffrorna lättare att hantera finns det dock en konvention där våglängden bara inverteras utan att bry sig om ljusets hastighet. Vi får ett "vågtal" i stället för en frekvens. Enheten är "inversen av längden". I IR-området råkar det vara bekvämt att tala om inversa centimeter (cm-1).

Interferometern

Så, vart leder detta oss? Jo, det råkar finnas en apparat som registrerar vågtalen i stället för våglängden. Den kallas interferometer och ser ut på följande sätt. Det är en lite konstig inställning vid första anblicken, men läs vidare och "ljuset skall uppenbaras":

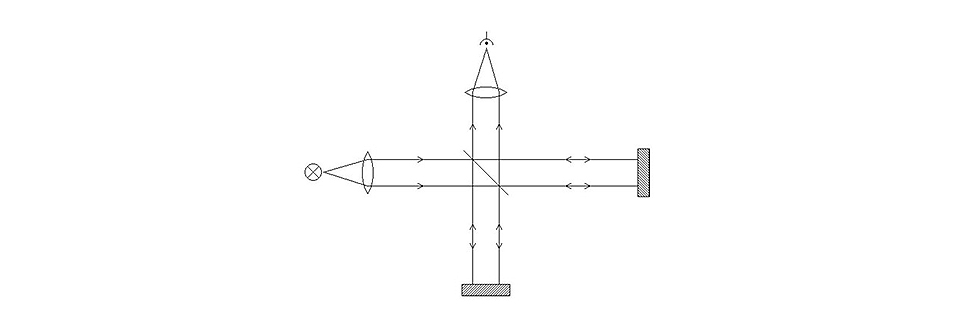
En Michelson-interferometer.

Det inkommande ljuset skickas genom en halvgenomskinlig spegel (en "stråldelare") som är monterad i 45 graders vinkel mot den inkommande ljusstrålen. 50 % av ljuset reflekteras, 50 % sänds genom spegeln. Var och en av de två utgående strålarna träffar sedan en 100 % reflekterande spegel och strålarna returneras i exakt samma riktning som de kom ifrån. Strålarna möts därför igen vid stråldelaren, där hälften av ljuset återigen reflekteras och hälften går igenom spegeln. Vi placerar en ljussensor i den återstående riktningen som går ut från stråldelaren.

Vad är då poängen med allt detta? Egentligen ingen alls så länge installationen är statisk, men låt oss flytta en av 100 %-speglarna något medan vi skickar in enfärgat (monokromatiskt) ljus och se vad som händer på sensorn:

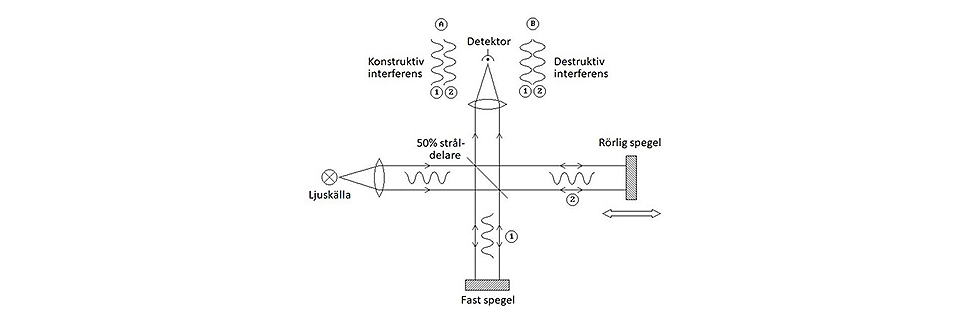
Konstruktiva och destruktiva interferenser.

Beroende på spegelpositionen kommer de två ljusstrålarna (tänk på dem som vågor) som går mot sensorn i vissa fall att samverka och ge en stark sensorsignal. Det kallas konstruktiv interferens. Men om spegeln flyttas bara en aning (en fjärdedel av våglängden för det inkommande ljuset) kommer de två vågorna i stället att upphäva varandra. Det kallas destruktiv interferens. Om vi nu flyttar spegeln med en fast hastighet får vi en sinusformad signal från sensorn. Den illustrerar ljusets frekvens, eller om man så vill vågtal, och kallas för "interferogram".

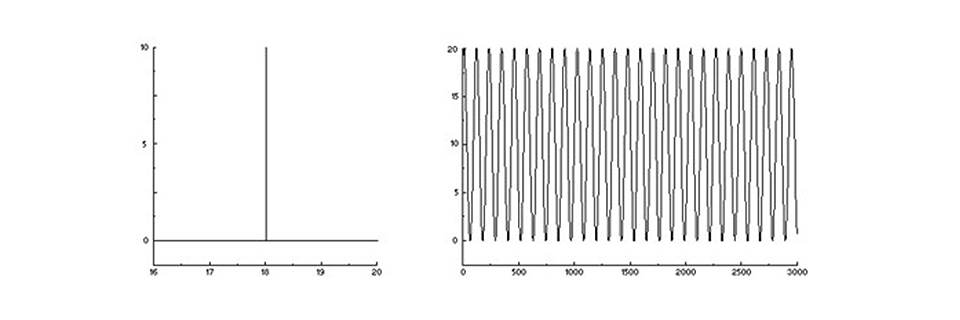
Ett monokromatiskt spektrum (vänster) och dess interferogram (höger) – bry dig inte om axelenheterna!

Interferogram

Om vi skickar in en något annorlunda färg (en annan våglängd) får vi fortfarande en sinusformad signal från sensorn, men med en något annorlunda period. Det är fortfarande ett interferogram, bara för en annan färg.
Låt oss nu göra det lite mer komplicerat och till exempel skicka in tre olika färger. Sensorn kommer att se summan av tre olika sinusvågor med lite olika perioder. Det är fortfarande konstruktiv interferens i vissa spegelpositioner och destruktiv i andra, men i ett mer komplext mönster. Ändå är det fortfarande interferogrammet för det inkommande trefärgsspektrumet.

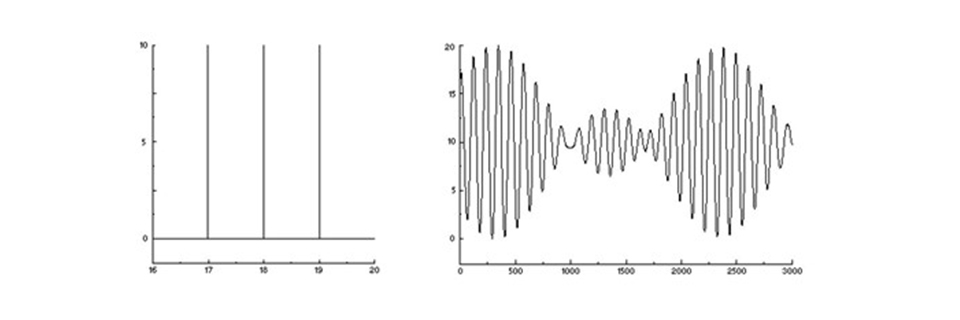
Ett trefärgsspektrum (vänster) och dess interferogram - tre adderade sinusvågor (höger).

Att skicka in monokromatiskt ljus eller till och med trefärgat ljus i en interferometer kan förklara hur den fungerar, men det är inte särskilt intressant ur spektroskopisk synvinkel. För att det ska bli användbart måste vi skicka in ljus från en källa med ett kontinuerligt emissionsspektrum där alla tänkbara våglängder (inom praktiska gränser) existerar samtidigt. Vad händer då?

Interferometern fortsätter att fungera som tidigare. Det är bara det att ett nästan oändligt antal våglängder genererar en sensorsignal som är baserad på summan av ett nästan oändligt antal sinusvågor. Signalen kan vara mycket komplex och kanske svår att föreställa sig, men det är fortfarande interferogrammet för det inkommande ljuset. Med ett kontinuerligt spektrum (inom ett visst våglängdsfönster) kan det se ut så här:

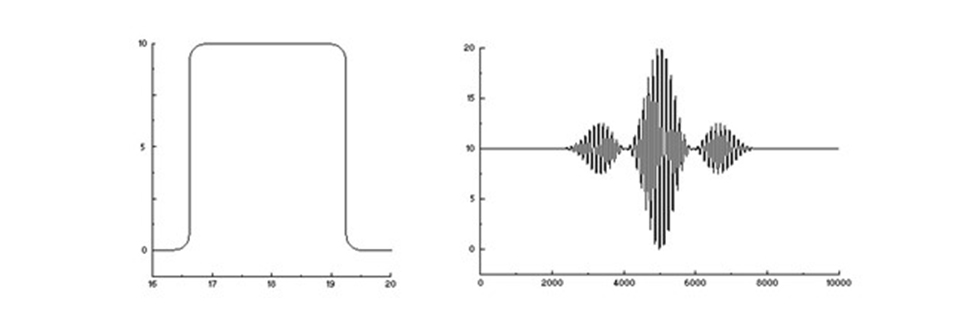
Ett kontinuerligt spektrum (vänster) och dess interferogram (höger).

Spektra och interferogram - två sidor av samma mynt

Genom att skanna interferometern kan vi alltså registrera ljusets interferogram och det uttrycks i vågtalsenheter. Jämför detta med att använda en spektrometer för att registrera ett spektrum, uttryckt i våglängdsenheter. Faktum är att interferogrammet och spektrumet för en specifik ljuskälla innehåller samma information om ljuset. Vi kan beskriva ljusets frekvens (vågtal) eller vi kan beskriva ljusets våglängd, men det är samma ljus vi talar om.

Vi har alltså interferogrammet, men för att tillämpa DOAS-tekniken behöver vi fortfarande spektrumet. Om vi tittar på ett "enfärgat" interferogram kan vi beräkna våglängden genom att bara invertera vågtalet. Men vad gör man med ett fullständigt, komplext bredbandigt interferogram? Svaret är en matematisk procedur som kallas Fouriertransform. Det skulle gå alldeles för långt att förklara hur den fungerar, men tänk bara på den som en "matematisk svart låda" (det är bara matematik i en dator, inte en fysisk enhet) som matas med interferogrammet och ut kommer spektrumet. Det fungerar faktiskt åt andra hållet också, men det är av mindre intresse i det här sammanhanget. Och nu när spektrumet äntligen är fastställt, förs det till DOAS-algoritmerna och de eftertraktade koncentrationerna av olika molekyler kan beräknas.

Omvägen - varför och när?

Ok, men... vad är poängen med allt det här? Varför inte använda en enkel spektrometer när slutprodukten ändå är ett spektrum? Svaret ligger i upplösningen i IR-området. Om vi vill ha låga detektionsgränser och hög noggrannhet vid mätning av gaskoncentrationer behöver vi absorptionsspektra med hög spektral upplösning. Vi började den här artikeln med att säga att spektrometern fungerar utmärkt i UV-området, men inte lika bra i IR-området. I vissa fall när vi vill mäta absorption i IR-området är spektrometern helt enkelt inte tillräckligt bra. Lyckligtvis är interferometern ett komplement till spektrometern. Den ger utmärkt spektral upplösning i IR-området vilket är precis vad vi är ute efter.

Tyvärr fungerar interferometern inte särskilt bra (i praktiken inte alls) i UV-området, men där har vi spektrometern för inspelning av högupplösta UV-spektra. I praktiska tillämpningar för gasövervakning är det inte ovanligt att man behöver detektera vissa gaser med sina eftersökta absorptionslinjer i UV-området och vissa med sina linjer i IR-området. Det är därför ganska vanligt med OPSIS-mätsystem med två olika instrument som arbetar parallellt, ett baserat på en spektrometer (en AR500 eller AR600) och ett annat baserat på en interferometer (en AR550 eller AR650).

Gasanalysatorerna med interferometrar inuti ("FTIR-DOAS-analysatorer") är mer komplexa än sina spektrometerbaserade syskon ("UV-DOAS-analysatorer"), men de är ändå släkt. Den förra tar en omväg via en interferometer och Fouriertransformen för att fastställa spektrumet, men de delar den grundläggande mätprincipen: att använda ljusabsorption för att fastställa koncentrationerna av föroreningar.